机器学习算法（二）—— 线性回归

1 线性回归简介

1.1 什么是线性回归

• 线性回归（Linear Regression）是一种用于建模两个或多个变量之间线性关系的统计方法。它通过拟合一条直线（或超平面）来描述自变量（输入特征）与因变量（输出目标）之间的关联，并可用于预测或分析变量间的影响关系。
• 假设因变量y与自变量x1,x2,…,xn之间的关系可以用如下线性方程表示：
  • y=β0+β1x1+β2x2+…+βnxn
    • β0：截距，模型在自变量全为0时的基准值
    • β1,β2,…,βn：自变量的系数，表示每个自变量对因变量的影响程度
• 通过估计这些系数，使模型预测值尽可能接近真实值。

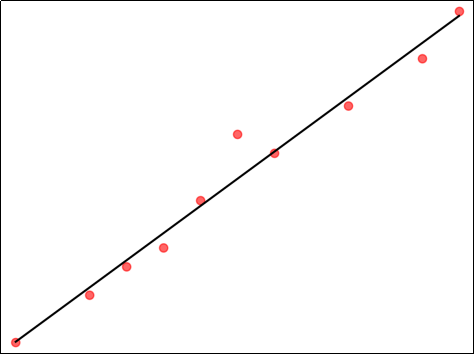
1.1.1 一元线性回归

仅有一个自变量：

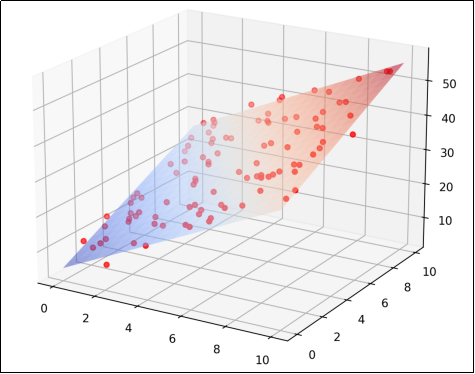
1.1.2 多元线性回归

包含多个自变量：

1.2 线性回归应用场景

• GDP预测：用历史数据（如投资、消费、出口）建立回归模型，预测GDP增长趋势。
• 广告效果评估：量化不同渠道广告投入对销售额的影响，优化预算分配。
• 药物剂量研究：分析药物剂量与患者生理指标（如血压、血糖）之间的关系。
• 产品质量控制：通过生产参数（温度、压力、原料配比）预测产品性能（如强度、耐久）。
• 政策效果评估：分析最低工资政策对就业率的影响，或环保法规对污染排放的抑制作用。
• 气候变化建模：用工业排放量、森林覆盖率等变量预测全球气温变化趋势。

1.3 API使用

例如，某中学教师想研究学生每周学习时间（小时）与数学考试成绩（0-100分）之间的关系，并预测学生成绩。

from sklearn.linear_model import LinearRegression

# 自变量，每周学习时长
X = [[5], [8], [10], [12], [15], [3], [7], [9], [14], [6]]
# 因变量，数学考试成绩
y = [55, 65, 70, 75, 85, 50, 60, 72, 80, 58]
# 实例化线性回归模型
model = LinearRegression()
# 模型训练
model.fit(X, y)
# 系数，每周每学习1小时，成绩会增加多少分
print(model.coef_)
# 截距
print(model.intercept_)
# 预测,每周学习11小时，成绩可能是多少分
print(model.predict([[11]]))

2 线性回归求解

2.1 损失函数

模型的预测值与真实值之间存在误差。

损失函数用于衡量模型预测值与真实值之间的误差，并通过最小化损失函数来优化模型参数。当损失函数最小时，得到的自变量系数就是最优解。

2.1.1 均方误差（MSE）

• n：样本个数。
• yi：第i个样本的真实值。
• f(xi)：第i个样本的预测值。

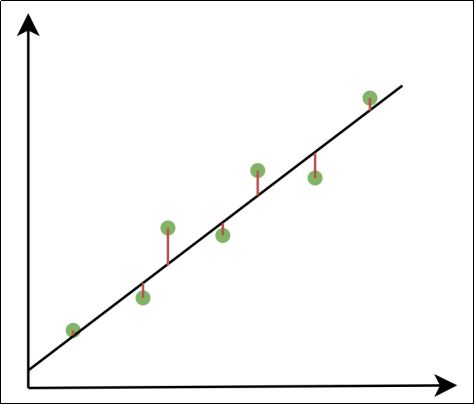
均方误差是回归任务中最常用的损失函数。均方误差对应了欧氏距离。基于均方误差最小化来进行模型求解的方法称为“最小二乘法”。在线性回归中，最小二乘法就是试图找到一条直线（或超平面），使所有样本到直线（或超平面）上的欧氏距离之和最小。

• 均方误差的特点
  • 均方误差对大误差比较敏感，因为平方项会放大较大的误差（如误差2→4，误差10→100）。
  • 均方误差是凸函数，存在全局的唯一最小值，平方项又使损失函数处处可导，便于求解最优参数。
  • 最小二乘法（最小化MSE）的解析解可通过矩阵运算直接求出（如）。
  • 若误差服从正态分布，则均方误差对应极大似然估计，是最优的损失函数。
• 误差服从正态分布时，均方误差与极大似然估计的关系
  • 假设因变量y与自变量x的关系为，为误差项。 当误差独立且具有相同分布，并且都服从正态分布时：

• 将 与 代入：

• 似然函数：

• 对数似然函数：

为使似然函数最大，需求解的最小值，发现其与均方误差直接相关。即最大化对数似然函数等价于最小化均方误差。

2.1.2 平均绝对误差（MAE）

平均绝对误差受异常值影响较小，但对小误差的惩罚较弱。适用与数据中存在显著异常值（如金融风险预测）的场景。

2.2 一元线性回归解析解

对于一元线性回归，有

对β0求偏导：

令偏导等于0：

对β1求偏导：

将代入：

令偏导等于0：

解得：

其中

所以

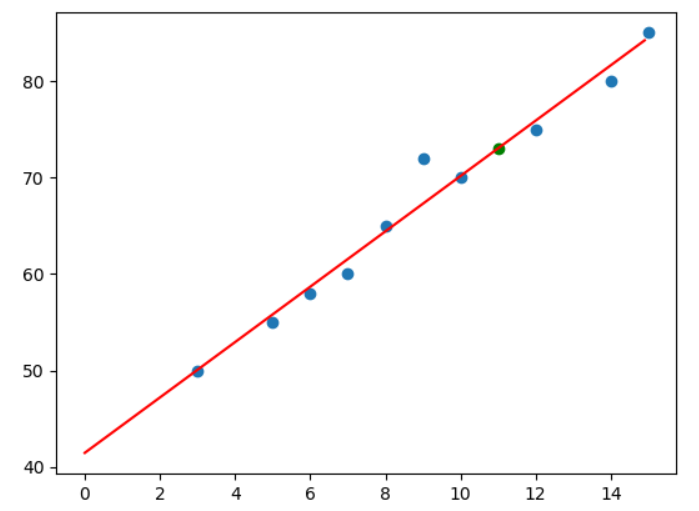
以前述学生每周学习时间（小时）与数学考试成绩（0-100分）之间的关系为例：

# 自变量，每周学习时长
X = [[5], [8], [10], [12], [15], [3], [7], [9], [14], [6]]
# 因变量，数学考试成绩
y = [55, 65, 70, 75, 85, 50, 60, 72, 80, 58]

解得